5.5 Elektroni

Etusivu ／ Luku 5: Mikroskooppiset hiukkaset

Lukijan opas: miksi ”piste-elektroni” venyttää intuitiota

Seuraavat ”pulmat” eivät ole laskennallisia virheitä vaan aukkoja rakenteellisessa ja alkuperää koskevassa intuitiossa. Ne selittävät, miksi esitämme materiaalisemman, rengasmaisen kuvan ja pysymme silti linjassa valtavirran numeroiden kanssa.

• Sähkövarauksen näkyvä alkuperä puuttuu: Pistemalli kohtelee varausta synnynnäisenä vakiona ”oikealla” suuruudella ja etumerkillä, mutta ei näytä, miksi näin on.
• Kvanttilukujen ”miksi”: Spin 1/2 ja varauksen kvantittuminen toimivat sääntöinä, mutta konkreettinen, materiaalinen mielikuva niiden luonteesta jää usein ohueksi.
• Lähi­kentän luettavuus on heikko: Kokeet suosivat kaukokenttää tai hyvin lyhyitä korkeaenergisiä ikkunoita, joissa piste­mäisyys korostuu. Harvoin visualisoidaan, miten lähi­kenttä on järjestynyt ja miten sähköinen sekä magneettinen liittyvät samaan geometriaan.
• Klassisen intuition painolasti: ”Pyörivä varattu pallo” törmää suhteellisuusteoriaan, säteilyhäviöihin ja korkeaenergisen sironnan rajoihin. Valtavirta hylkää kuvan, mutta lukija luisuu siihen helposti.
• Säteilyn takaisinkytkennän selitysvaje: Kvanttikuvauksessa asiat toimivat; puhtaasti klassisissa yhtälöissä ”ennakko­kiihtyvyys” ja ”karkaavat ratkaisut” herättävät toiveen mediumiin ja muistiin nojaavasta intuitiivisesta tulkinnasta.

Pistekieli on numeerisesti hyvin menestyksekästä. Energiasäieteorian (EFT) rengaskieli pyrkii täydentämään kuva­tason, ei kumoamaan numeroita. Seuraavassa on kokoonpanon kuvaus Energiasäieteorian mukaan.

Ydinajatus (lukijaystävällinen versio)

Kuvassa ”energiasäie energiameressä” elektroni ei ole abstrakti piste, vaan yksi energiasäie, joka sulkeutuu renkaaksi ja pysyy koossa itseään kannattelevana kolmiulotteisena kudoksena energiameressä. Renkaalla on äärellinen paksuus. Sen poikkileikkauksessa kiertää vaiheeseen lukittunut spiraalivirtaus: vahvempi sisäsivulla, heikompi ulkosivulla. Tämä lähi­kentän rakenne kaivertaa väliaineeseen sisäänpäin suuntautuvan orientaatiotekstuurin—tämä on Energiasäieteoriassa negatiivisen varauksen operatiivinen määritelmä. Samaan aikaan renkaan suuntainen lukittunut signaali ja orientaation aikakeskiarvo (lievä preessio ja pieni värinä, ei jäykkää 360° pyörimistä) silottavat kaukaisen vaikutuksen lähes isotrooppiseksi, lempeäksi vetovoimaksi—tämän luemme massaksi. Suljettu sisäinen kierto ja sen kadenssi ilmenevät elektronin spininä ja magneettisena momenttina.

Huom.: ”Juoksevilla vaihekaistoilla” tarkoitetaan kuviokaaren etenemistä, ei aineen tai informaation valoa nopeampaa kuljetusta.

I. Miten elektroni ”solmii” itsensä: yksirengas, suljettu ja spiraalinen poikkileikkaus

1. Perusnäkymä: Sopivalla tiheydellä ja ”jännityksellä” energiameri nostaa säikeen esiin; säie valitsee vähätyöisimmän reitin ja sulkeutuu yhdeksi renkaaksi, joka on pitkäikäisempi.
2. Ei jäykkä vanne: Renkaalla on paksuutta ja kimmoisuutta; geometria ja jännitys tasapainottuvat, mikä tuottaa vakauden.
3. Spiraali poikkileikkauksessa: Vaihe kiertää lukittuna spiraalina: sisällä viipyminen on pidempi, ulkona lyhyempi. Kuviota ei ole ”jäädytetty”—vaihekaista juoksee jatkuvasti ja nopeasti.
4. Nopea renkaan suunnassa, hidas orientaatiossa: Renkaan kadenssi on nopea; globaali orientaatio preessaa hitaasti ja värisee hienovaraisesti. Aikakeskiarvon jälkeen kaukoulkonäkö on lähes akselisymmetrinen, ilman tarvetta olettaa jäykkää pyörimistä.
5. Polariteetin alkuperä ja diskreetit vihjeet:
   • Negatiivisen määritelmä: Lähi­kentän tekstuuri osoittaa sisäänpäin renkaaseen katselukulmasta riippumatta—tämä määrittää negatiivisen varauksen.
   • Positiivisen peilikuva: Jos lukitus vaihtuu (ulkona vahva, sisällä heikko), nuolet osoittavat ulospäin: positiivinen varaus; vasteet peilaavat etumerkkiä samassa ulko­kentässä.
   • Diskreetit portaat: Spiraali ja renkaan suuntainen lukitus sallivat vain tietyt vakaimmat askelmäärät ja kudontatavat. Perusaskel antaa yhden negatiivisen varausyksikön; monimutkaisemmat ovat energiakalliita ja harvoin pysyviä.
6. Vakausikkuna: ”Elektroniksi” tuleminen edellyttää samanaikaisesti renkaan sulkeutumista, itsejännityksen tasapainoa, vaihelukitusta, sopivaa mittakaavaa ja energiaa sekä ympäristön leikkausrasituksen pysymistä kynnyksen alla. Useimmat yritykset purkautuvat nopeasti mereen; harvat osuvat vakausikkunaan ja elävät pitkään.

II. Massan ulkoasu: symmetrinen ”matalasyvyinen allas”

1. Jännityskartta: Renkaan asettaminen energiamereen on kuin painaisi matalan, symmetrisen altaan kireään kalvoon: suurin jännitys renkaan tuntumassa, nopea tasoittuminen ulospäin.
2. Miksi luemme tämän massaksi:
   • Inertia: Elektronin työntäminen raahaa altaan ja väliaineen mukaan; vastaveto tulee joka suunnasta. Tiiviimpi rengas tekee syvemmän, vakaamman altaan—suurempi inertia.
   • Ohjaus (gravitaation kaltainen): Sama rakenne piirtää jännityskartan uudelleen lempeäksi kaltevuudeksi kohti elektronia, jota pitkin hiukkaset ja aaltopaketit ohjautuvat helpommin.
   • Isotropia ja ekvivalenssi: Kaukana ulkoasu on tasapuolinen ja isotrooppinen, ekvivalenssiperiaatteen ja makromittaisten testien mukainen.
   • Tilastollinen jännitysgravitaatio: Monien tällaisten mikro­rakenteiden aika-avaruus­keskiarvo tuottaa lempeän, yhtenäisen kollektiivisen ohjauksen.

III. Varauksen ulkoasu: ”sisäänpäin kiertyvä” lähi­kenttä ja koossapysyvyys keski­kentässä

Konventio: Sähkökenttä on orientaatiotekstuurin säteittäistä jatketta; magneettikenttä on renkaan suuntainen kiertyminen, joka syntyy siirtymäliikkeestä tai sisäisestä suljetusta kierrosta. Lähde on sama lähi­kentän geometria, roolijako on eri.

• Sisäänpäin kiertyminen lähellä: ”Sisällä vahva, ulkona heikko” kaivertaa energiamereen sisäänpäin suuntautuneen tekstuurin. Ohittava rakenteinen olio kokee pienemmän vastuksen, jos orientaatiot sopivat (vetää), ja suuremman, jos eivät sovi (hylkii). Pelkkä häiriö­aaltopaketti tuntee tämän vähemmän; massa-allas hallitsee.
• Liike ja magnetismi: Siirtyessä lähi­tekstuuria vetäytyy mukaan, ja reitin ympärille muodostuu renkaan­suuntainen pyörre—magneettikenttä. Myös ilman siirtymistä sisäinen lukittu kierto järjestää paikallisen pyörteen, joka antaa magneettisen momentin. Väärinymmärrysten välttämiseksi puhumme ekvivalentista rengasvirrasta/rengasvuosta, joka on geometristen säteiden riippumaton; korkeilla energioilla ja lyhyillä ajoilla ulkoasu palaa liki pisteeksi.
• Hälyn hienosäätö: Energiameren taustahäly säätää hienosti sisäänpäinkierron voimakkuutta. Jos ilmiö on mitattavissa, sen tulee olla käännettävissä, toistettavissa ja kytkettävissä päälle/pois hallituilla gradientilla, ja sen on pysyttävä selkeiden ylärajojen sisällä.

IV. Spin ja magneettinen momentti: yksirenkaan ”kadenssi” ja ”lukitus” (vahvistettu)

• Spin intuitiivisesti: Spin on näkyvä kätisyys suljetussa vaihe­kadenssissa. Se ilmenee ajan keskiarvona eikä edellytä jäykkää kappalepyörimistä.
• Momentin alkuperä ja suunta: Magneettinen momentti kumpuaa ekvivalentista rengasvirrasta/rengasvuosta, joka on säde­riippumaton; korkea energia/lyhyt aika palauttaa pistemäisen ulkoasun. Suuruuteen ja suuntaan vaikuttavat renkaan suuntainen kadenssi, poikkileikkauksen ”sisällä vahva/ulkona heikko” -bias sekä lähi­tekstuurin järjestys.
• Preessio ja vaste ulko­kentissä: Kun ulkoinen orientaatio­alue muuttuu, spin preessaa, ja energiatason siirtymät sekä viivamuodot ovat kalibroitavissa; nopeuden määräävät sisäisen lukituksen vahvuus ja kenttä­gradientit.

V. Kolme päällekkäistä näkymää: yksittäinen donitsi­rengas → pehmeäreunainen tyyny → symmetrinen matala allas

• Läheltä (mikro): Yksi donitsi­rengas, rengasvyö kirein. ”Sisällä vahva/ulkona heikko” spiraali on selkeä; sisäänpäin osoittava lähi­tekstuurin suunta lukitsee negatiivisen varauksen.
• Keskeltä (siirtymäkerros): Pehmeäreunainen tyyny, joka tasoittuu nopeasti ulospäin. Pidemmällä aikaikkunalla hienokuviot silottuvat, siirtymä pehmenee, varausjakauma koheesioituu.
• Kaukaa (makro): Symmetrinen matala allas, yhtä syvä kaikkialla—vakaa, isotrooppinen massa­ulkoasu.

Kuvitusankkurit: ”lyhyt johtava kaari + jälkivana” vaihe­rintamasta, ”lähi­kentän nuolet sisäänpäin”, ”siirtymätyynyn ulkoreuna”, ”altaan suu ja tasasyvyiset renkaat”; selite: ”ekvivalentti rengasvirta (säde­riippumaton)”, ”isotropia ajan keskiarvon jälkeen”.

VI. Mittakaava ja havaittavuus: hyvin pieni ydin, mutta ”sivu­profiili” on mahdollinen

• Erittäin kompakti ydin: Ydin­käämi on erittäin tiukka, suora kuvantaminen on vaikeaa. Korkeaenergiaiset, hyvin lyhyet sironnat antavat yleensä liki piste­vastetta.
• Tehokkaan varaussäteen sivuprofiili: Sisään­kierto ja keski­kentän koheesio viittaavat tehokkaaseen varausjakautumaan, joka hakeutuu rengasalueelle. Tarkka elastinen sironta ja polarisaatio­mittaukset voivat sivu­profioida tätä ”tehokasta sädettä”.
• Pisteraja (kova sitoumus): Nykyisissä energia- ja aikaikkunoissa muotokerroin tulee romahtaa piste­ulkoasuun, ilman lisä­resolvoituvia kuvioita; ”tehokas säde” muuttuu energian kasvaessa erottumattomaksi.
• Pehmeä siirtymä: Läheltä kauas on vähittäistä silottumista. Kaukana nähdään vain vakaa allas, ei juoksevia vaihekaistoja.

VII. Synty ja annihilaatio: miten se ilmestyy ja katoaa

• Synty: Korkea jännitys ja tiheys avaavat poikkileikkauksen spiraalille ”käämintä­ikkunan”. Kun rengas sulkeutuu ja lukittuu muotoon sisällä vahva/ulkona heikko, negatiivinen varaus lukittuu samanaikaisesti; käänteisenä syntyy positroni.
• Annihilaatio: Kun elektroni ja positroni lähestyvät, niiden vastakkaismerkkiset lähi­virvelit kumoavat toisensa. Suljettu verkko purkautuu hyvin nopeasti, jännitys palaa energiamereen aaltopaketteina, havaittuna valona tai muina häiriöinä; energia ja impulssi säilyvät termi termiltä säikeen ja meren välillä.

VIII. Vertailu moderniin teoriaan

1. Missä se täsmää:
   • Varauksen kvantittuminen ja identtisyys: Peruslukitus ”sisällä vahva/ulkona heikko” vastaa yhtä negatiivisen varauksen yksikköä, kuten havaitaan.
   • Spin ja magneettinen momentti yhdessä: Suljettu sisäkierto ja kadenssi kytkevät spinin ja momentin luontevasti.
   • Pistemäinen sironnassa: Pieni ydin ja voimakas aikakeskiarvo tekevät korkeaenergisestä sironnasta liki piste­mäisen.
2. Uusi ”materiaalikerros”:
   • Varauksen alkuperäkuva: Negatiivinen varaus asettuu suoraan poikkileikkauksen säteittäiselle biasille (sisällä vahva/ulkona heikko), joka kaivertaa sisäänpäin suuntautuvan tekstuurin—ei ”jälkikäteen liimattu tunniste”.
   • Massan ja ohjauksen yhdistetty kuva: Symmetrinen allas + aikakeskiarvo asettavat lähi­kentän anisotropian ja kauko­kentän isotropian samalle kankaalle.
   • Sähkö ja magnetismi samassa geometriassa: Sähköinen on säteittäinen jatke, magneettinen renkaan suuntainen kierto—kaksi roolia yhdestä lähi­geometriasta, samassa aikaikkunassa.
3. Johdonmukaisuus ja reunaehdot:
   • Korkeaenerginen yhdenmukaisuus: Nykyisissä E/t-ikkunoissa muotokerroin tulee näyttää piste­mäiseltä; ”tehokas säde” katoaa erotuskyvystä energian myötä.
   • Magneettisen momentin vertailuarvot: Pääarvo ja suunta sopivat mittauksiin; mahdolliset ympäristö­riippuvat mikro­poikkeamat ovat käännettävissä, toistettavissa, kalibroitavissa ja nykyisten epävarmuuksien alapuolella.
   • Lähes nolla sähköinen dipolimomentti (EDM): Homogeenisessa ympäristössä lähes nolla; hallittu jännitys­gradientti saa aikaan hyvin heikon lineaarisen vasteen, selvästi nykyrajojen alle.
   • Spektroskopia säilyy: Vetytyyppiset spektrit, fine/hyperfine-siirtymät ja interferenssi pysyvät kokeellisen virheen rajoissa; uudet piirteet vaativat riippumattoman, testattavan lähteen ja selkeät on/off-kriteerit.
   • Dynaaminen vakaus: Ei ”vaikutusta ennen syytä” eikä itsekiihtymistä. Mahdollinen dissipaatio ilmenee meren ja säikeen kausaalisena muistillisen kytkennän kautta, kalibroitavin aikaikkunoin ja ristiriidatta havaintojen kanssa.

IX. Luettavat vihjeet: kuva­taso | polarisaatio | aika | energia­spektri

• Kuva­taso: Sädekimppujen kaareutuminen ja sisäreunan vahvistus (jos havaittavissa) heijastavat altaan geometriaa ja koheesiivista varausjakaumaa.
• Polarisaatio: Polarisoidussa sironnassa etsi polarisaatiokaistoja ja vaihe-eroja, jotka sopivat ”sisäänpäin suuntautuvan tekstuurin” kanssa—lähi­kentän geometrinen sormenjälki.
• Aika: Impulssi­ärsyke paikallisen kynnyksen yli voi synnyttää portaita ja kaiun; aika­skaalat seuraavat lukituksen vahvuutta.
• Spektri: Jälkikäsittelevissä ympäristöissä voi esiintyä yhtä aikaa pehmeän segmentin nousu ja kapeat kovat huiput, jotka liittyvät ”sisällä vahva/ulkona heikko” -rakenteeseen; pienet siirtymät/halkeamat voivat johtua lukituksen vahvuuden hienosäädöstä taustahälyllä.

X. Ennusteet ja testit: lähi- ja keski­kentän operatiiviset koejärjestelyt

• Etumerkin peilikäännös keraalisessa lähi­sironnassa
  Ennuste: Käännä anturin keraalisuus tai vaihda elektroni ↔ positroni—vaihesiirtymät kääntyvät pareittain.
  Järjestely: Yksihiukkasansat + vaihdettavat mikroaalto/optiset tilat, joilla on radallinen kulmamomentti (OAM).
  Kriteeri: Käännettävä inversio ja vakaa amplitudi.
• ”Tehokkaan g-kertoimen” ympäristö­lineaarinen drift
  Ennuste: Hallittu jännitys­gradientti aiheuttaa pienen lineaarisen drifitin syklotroniresonanssin taajuudessa; positronilla kulmakerroin on vastamerkkinen.
  Järjestely: Erittäin vakaat magneettiansat + mikromassapalikat/mikro­kaivokentät gradientin kalibrointiin.
  Kriteeri: Ensimmäisen kertaluvun verrannollisuus gradienttiin; peilattu käyttäytyminen e/e⁺.
• Lähes nolla EDM ja gradientin indusoima lineaarinen vaste
  Ennuste: Lähes nolla tasaisessa ympäristössä; gradientti synnyttää hyvin heikon, käännettävän vasteen.
  Järjestely: Ioniansat/molekyylisuihkut, päälle ekvivalentti jännitys­gradientti; luku resonanssivaihemenetelmällä.
  Kriteeri: On/off ja suunnan kääntö gradientin mukana; amplitudi nykyrajat alittava.
• Epä­symmetrinen läpäisy keraalisten nanohuokosten läpi
  Ennuste: Esipolarisoitua spiniä kantava elektroni keraalisen rajan yli näyttää hyvin pienen vasen–oikea-epäsymmetrian; positronilla etumerkki kääntyy.
  Järjestely: Keraaliset nanokalvot, monikulma- ja monienergia­skannaukset.
  Kriteeri: Epäsymmetria­termi kääntyy kalvon keraalisuuden ja hiukkasen polariteetin mukana.
• Hieno vinouma säteilyssä vahvoissa kentissä
  Ennuste: Voimakkaasti kaareutuvissa kentissä säteilykulmat näyttävät pienen, toistettavan vinouman, joka sopii sisään­tekstuurin kätisyyteen.
  Järjestely: Vertaa polarisaatiota ja kulmajakautumaa e/e⁺ varastorenkaissa, tai mittaa takaiskusäteilyn geometria erittäin voimakkailla lasereilla.
  Kriteeri: Energia­kalibroitavat erot sekä etumerkin kääntyminen polariteetin vaihtuessa.

XI. Lyhyt sanasto (lukijaystävällinen)

• Energiasäie: Vaiheen ja jännityksen viivamainen kantaja, jolla voi olla paksuutta.
• Energiameri: Taustaväliaine, joka antaa palauttavan vasteen ja orientaatio­reaktion.
• Jännitys/orientaatiotekstuuri: Suunta ja voimakkuus, jolla väliaine ”pingottuu/vetäytyy”.
• Vaihelukitus: Vaiheet ”pureutuvat kuin hammasrattaat”, mikä ylläpitää vakaata kadenssia.
• Lähi/keski/kauko­kenttä: Kolme vyöhykettä renkaasta ulospäin; kauempana silottuminen vahvistuu aikakeskiarvosta.
• Aikakeskiarvo: Pienet, nopeat vaihtelut tasoittuvat havaintoikkunassa, ja jäljelle jää vakaa ulkoasu.

XII. Yhteenvetona

Energiasäieteoriassa elektroni on renkaaksi sulkeutuva energiasäie: lähi­kentässä sisäänpäin suuntautuva orientaatio­tekstuurin määrittää negatiivisen varauksen; keski- ja kauko­kentissä symmetrinen matala allas näyttää vakaan massa­ulkoasun. Spini ja magneettinen momentti syntyvät luonnostaan suljetusta kierrosta ja kadenssista. Kuvalla ”yksi donitsi­rengas → pehmeäreunainen tyyny → symmetrinen matala allas” yhdistämme lähi-, keski- ja kauko­tason yhdeksi kokonaisuudeksi ja ankkuroimme sen olemassa olevaan kokeelliseen tietoon selkeiden reunaehtojen kautta.

XIII. Kuviot (Kuvio 1: Elektroni; Kuvio 2: Positroni)

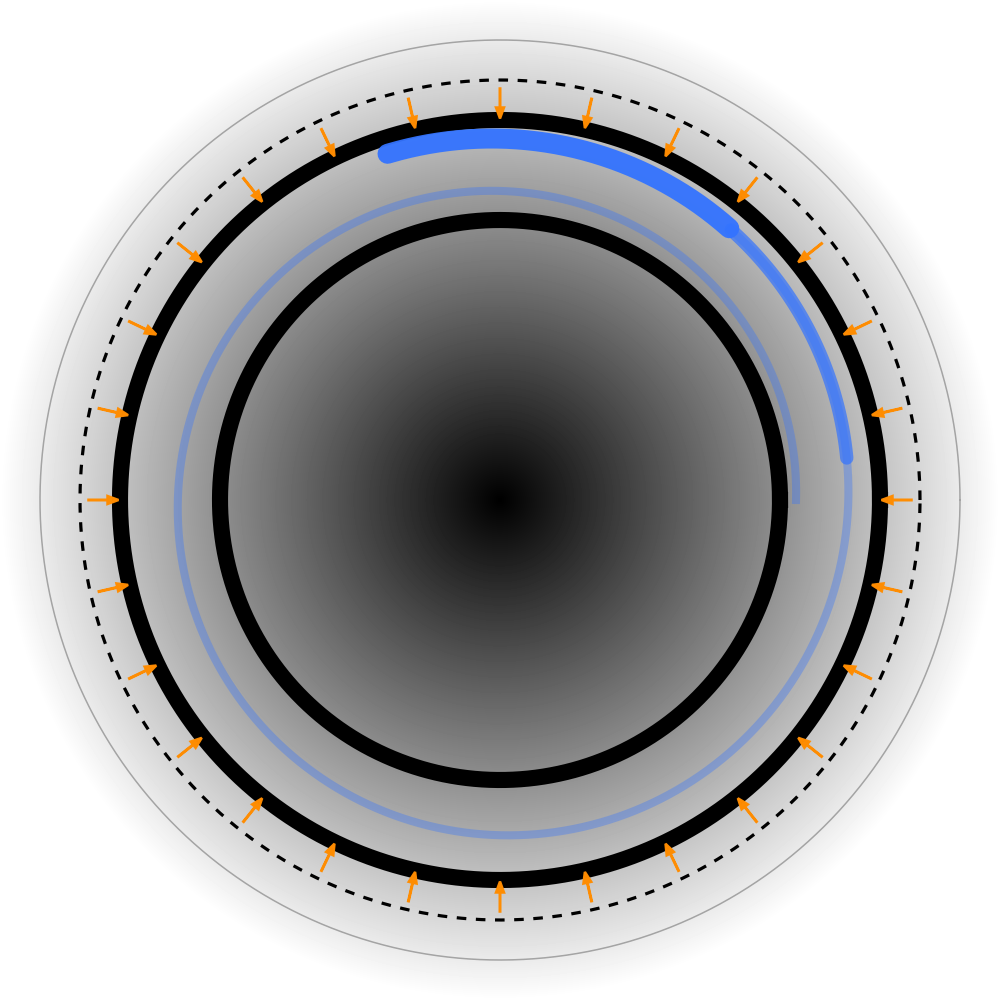
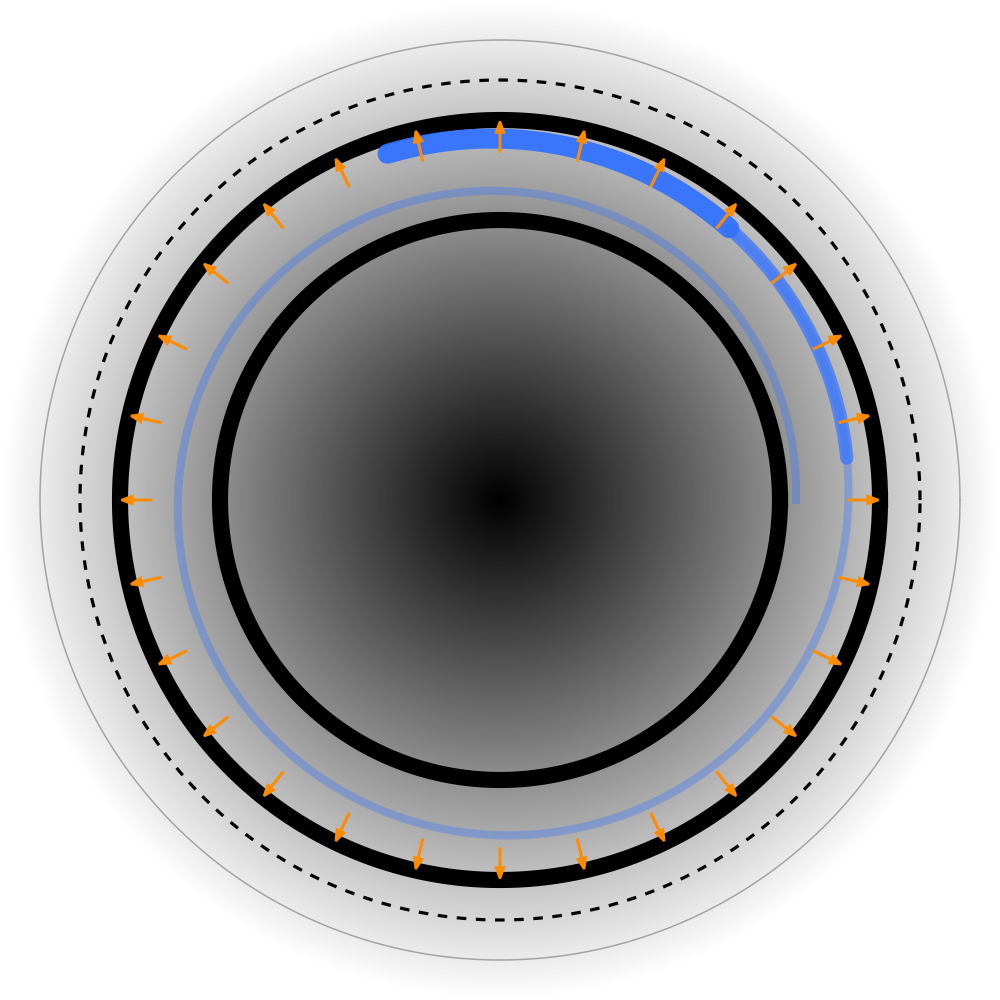
1. Runko ja paksuus
   • Yksi suljettu päärengas: Yksi säie sulkeutuu yhdeksi renkaaksi; kaksoisviiva tarkoittaa itseään kannattelevaa paksuutta, ei kahta säiettä.
   • Ekvivalentti rengasvirta/rengasvuon: Magneettinen momentti johtuu ekvivalentista rengasvirrasta, ei siitä, että päärengas olisi geometrinen ”virtasilmukka”.
2. Vaihe­kadenssi (ei rata; sininen spiraali renkaan sisällä)
   • Sininen spiraalinen vaihe­rintama: Piirrä sininen spiraali sisä- ja ulkoreunan väliin merkitsemään hetkellistä vaihe­rintamaa ja lukittua kadenssia.
   • Hiipuva häntä → vahva kärki: Ohut, vaalea häntä ja paksu, tumma kärki näyttävät kätisyyden ja ajan suunnan; tämä merkitsee kadenssia, ei hiukkasrataa.
3. Lähi­kentän orientaatio­tekstuurin (määrittää varauksen polariteetin)
   • Säteittäiset oranssit mikro­nuolet: Kehrä lyhyitä oransseja nuolia juuri renkaan ulkopuolelle, osoittamaan sisään—negatiivisen varauksen lähi­tekstuurin. Mikrotasolla vastus on pienempi nuolien suuntaan ja suurempi vastakkaiseen suuntaan—vetovoiman/poistovoiman lähde.
   • Positronin peili: Positroni­kuvassa nuolet osoittavat ulos; vaste kääntää etumerkin.
4. Keski­kentän ”siirtymätyyny”
   Pehmeä katkoviivakehä: Ilmaisee kerroksen, joka koostaa ja silottaa lähi­yksityiskohdat—anisotropia hiipuu.
5. Kauko­kentän ”symmetrinen matala allas”
   Keskeinen liukuvarjostus/tasasyvyiset renkaat: Käytä lempeää konsentrista varjostusta ja katkoviivaisia tasasyvyys­renkaita akselisymmetrisen vedon näyttämiseen—vakaa massa­ulkoasu, ilman pysyvää dipolivinoamaa.
6. Ankkurimerkinnät
   • Sininen spiraalinen vaihe­rintama (renkaan sisällä).
   • Lähi­kentän säteittäisten nuolten suunta.
   • Siirtymätyynyn ulkoreuna.
   • Altaan suu ja tasasyvyys­renkaat.
7. Huomioita lukijalle
   • ”Juoksevat vaihekaistat” seuraavat kuviokaaren etureunaa, eivät ylivaloista ainetta tai tietoa.
   • Kaukoulkonäkö on isotrooppinen, ekvivalenssiperiaatteen ja havaintojen mukainen; nykyisissä E/t-ikkunoissa muotokerroin tulee konvergoida piste­ulkoasuun.